Enunciado del Segundo Parcial de Álgebra y Geometría Analítica [31-10-2015]
Resolución en video
Ejercicio 1
Ejercicio 2
Ejercicio 3
Ejercicio 4
Ejercicio 5
Resolver la siguiente ecuación en \(\mathbb{C}\): \({x^3} + \frac{{1 + i}}{{1 – i}} = 0\)
RESOLUCIÓN
Despejamos \({x^3}\) y realizamos la división de complejos multiplicando y dividiendo por el conjugado del denominador:
\[{x^3} = – \frac{{1 + i}}{{1 – i}}.\left( {\frac{{1 + i}}{{1 + i}}} \right) = – \frac{{1 + 2i + {i^2}}}{{1 – {i^2}}} = – \frac{{2i}}{2} = – i\]
Debemos hallar entonces las raíces cúbicas de \( – i\).
\( – i\) es el complejo de módulo 1, y argumento principal \(\frac{3}{2}\pi \).
Lo escribimos en forma trigonométrica:
\[{x^3} = – i = 1.\left( {\cos \left( {\frac{{3\pi }}{2}} \right) + isen\left( {\frac{{3\pi }}{2}} \right)} \right)\]
Ahora aplicamos la fórmula de las raíces enésimas de un complejo (leer más sobre esto acá):
\[\sqrt[3]{{ – 1}} = \sqrt[3]{{\left| { – 1} \right|}}.\left( {\cos \left( {\frac{{Arg\left( { – 1} \right) + 2k\pi }}{3}} \right) + i.{\rm{sen}}\left( {\frac{{Arg\left( { – 1} \right) + 2k\pi }}{3}} \right)} \right)\;\;\;\;\;k = 0,1,2\]
\[{x_k} = 1\left( {\cos \left( {\frac{{\frac{{3\pi }}{2} + 2k\pi }}{3}} \right) + isen\left( {\frac{{\frac{{3\pi }}{2} + 2k\pi }}{3}} \right)} \right){\rm{\;\;\;\;\;}}k = 0,1,2\]
\[{x_0} = 1\left( {\cos \left( {\frac{\pi }{2}} \right) + isen\left( {\frac{\pi }{2}} \right)} \right) = i\]
\[{x_1} = 1\left( {\cos \left( {\frac{{7\pi }}{6}} \right) + isen\left( {\frac{{7\pi }}{6}} \right)} \right) = – \frac{{\sqrt 3 }}{2} – \frac{1}{2}{\rm{\;\;i\;}}\]
\[{x_2} = 1\left( {\cos \left( {\frac{{11\pi }}{6}} \right) + isen\left( {\frac{{11\pi }}{6}} \right)} \right) = \frac{{\sqrt 3 }}{2} – \frac{1}{2}\;i\]
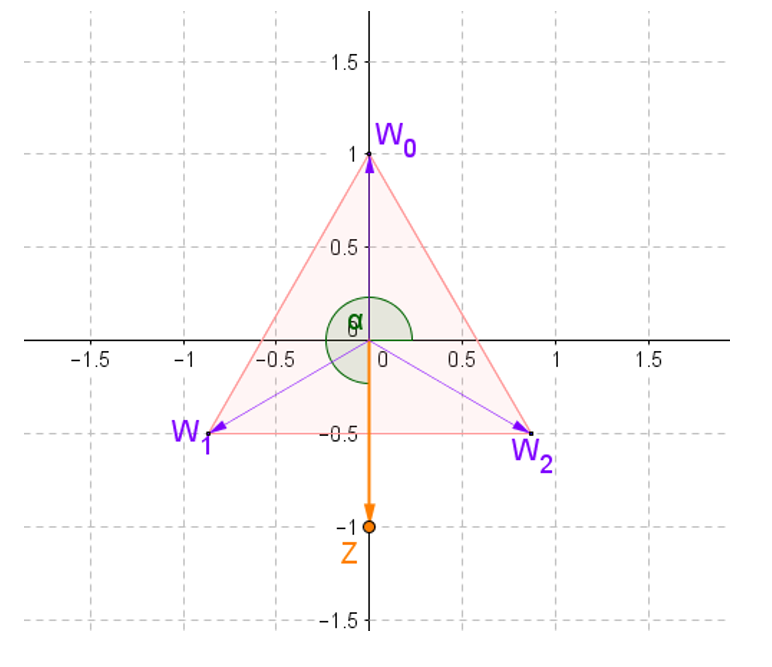
Entonces el conjunto solución es:
\[S = \left\{ {i,\frac{{\sqrt 3 }}{2} – \frac{1}{2}\;i, – \frac{{\sqrt 3 }}{2} – \frac{1}{2}{\rm{\;\;i\;}}} \right\}\]


