¿Qué se necesita para definir una transformación lineal?
Consideremos el siguiente triángulo en \({\mathbb{R}^2}\):
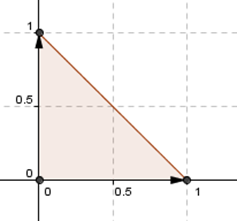
¿Existirá alguna transformación lineal que permita modificar de cierta manera este triángulo? Por ejemplo, una \(F\) que transforme el triángulo dado en este otro:
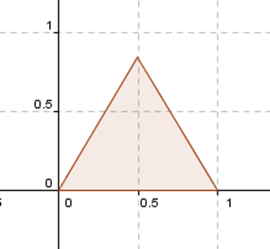
O alguna que lo transforme así:
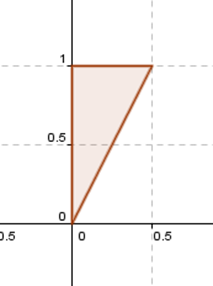
O un movimiento como éste:
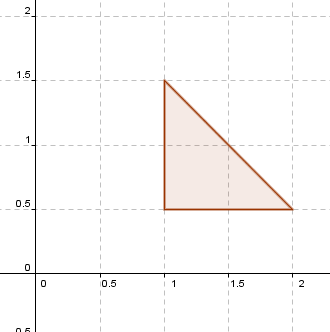
El triángulo 4 no contiene al (0,0), por lo tanto no puede obtenerse aplicando una transformación lineal al triángulo 1. ¿Por qué?
¿Los otros podrán obtenerse mediante una transformación lineal? ¿Existe alguna herramienta teórica que permita asegurarlo?
Sí, es el teorema fundamental de las transformaciones lineales.
Teorema fundamental de las transformaciones lineales
Este teorema, conocido también como «Teorema de existencia y unicidad de una transformación lineal», dice lo siguiente:
Para demostrarlo habría que demostrar que esa transformación existe, que es única, y que es lineal. No lo vamos a demostrar pero lo pueden encontrar en textos de álgebra lineal. En el texto recomendado de Ana María Kozak y otros autores, Nociones de Geometría Analítica y Algebra Lineal, está en página 561 y siguientes.
Ejemplo 1
Sean \(V = {\mathbb{R}^2}\) y \(W = {\mathbb{R}^3}\) Consideremos en la base \(B = \left\{ {\left( {1,0} \right),\left( {1,1} \right)} \right\}\), y sean \({w_1} = {w_2} = \left( {0,1,0} \right)\) De acuerdo con el teorema, existe una única transformación lineal \(T:{\mathbb{R}^2} \to {\mathbb{R}^3}\) que verifica: \[T\left( {\left( {1,0} \right)} \right) = \left( {0,1,0} \right)\] \[T\left( {\left( {1,1} \right)} \right) = \left( {0,1,0} \right)\] ¿Cómo buscamos la fórmula de la transformación lineal? Tomamos un vector genérico de \({\mathbb{R}^2}\) y lo escribimos como combinación lineal de la base, o sea buscamos sus coordenadas respecto de B: \[\left( {x,y} \right) = \alpha \left( {1,0} \right) + \beta \left( {1,1} \right) \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x = \alpha + \beta }\\{y = \beta }\end{array}} \right. \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{\alpha = x – y}\\{\beta = y}\end{array}} \right.\] Los escalares \(\alpha ,\beta \) son las cordenadas del vector \(\left( {x,y} \right)\) en la base \(B\): \[{\left[ {\left( {x,y} \right)} \right]_B} = \left( {\begin{array}{*{20}{c}}{x – y}\\y\end{array}} \right)\] Donde recordemos que la escritura \({\left[ {\left( {x,y} \right)} \right]_B}\) significa «las coordenadas del vector \(\left( {x,y} \right)\) en la base . \[\left( {x,y} \right) = \alpha \left( {1,0} \right) + \beta \left( {1,1} \right)\] Aplicamos la transformación lineal a ambos miembros: \[ \Rightarrow {\rm{\;}}T\left( {x,y} \right) = T\left( {\alpha \left( {1,0} \right) + \beta \left( {1,1} \right)} \right)\] Por las propiedades de las transformaciones lineales, Reemplazamos \(\alpha \) y \(\beta \) : \[T\left( {x,y} \right) = \left( {x – y} \right).\left( {0,1,0} \right) + y\left( {0,1,0} \right)\] \[T\left( {x,y} \right) = \left( {0,x – y,0} \right) + \left( {0,y,0} \right)\] \[T\left( {\left( {x,y} \right)} \right) = \left( {0,x,0} \right)\] Hemos obtenido la fórmula de la transformación lineal que cumple con las condiciones.
Ejemplo 2
Vamos a ver si podemos transformar el triángulo del esquema de la izquierda, en el triángulo del esquema que está a la derecha:
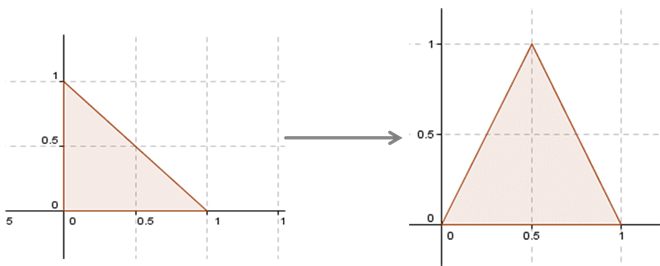
Nosotros tenemos que dar una base de \({\mathbb{R}^2}\) y asignarle sus transformados.
Por ejemplo consideremos los versores canónicos que definen al primer triángulo: 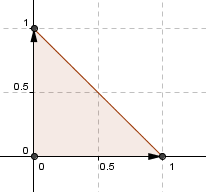
Entonces podríamos hacer la siguiente asignación:
\[F\left( {\left( {1,0} \right){\rm{\;}}} \right) = \left( {1;0} \right)\] \[F\left( {\left( {0,1} \right){\rm{\;}}} \right) = \left( {\frac{1}{2};1} \right)\]
Como \(\left( {1,0} \right),\;\left( {0,1} \right)\) constituyen una base del dominio, el teorema fundamental permite afirmar que existe una única transformación lineal que verifica esto:

Para encontrar la fórmula de esta trasformación vamos a escribir a un vector genérico de \({\mathbb{R}^2}\) como combinación lineal de los vectores de la base dada: \[\left( {x,y} \right) = \alpha \left( {1,0} \right) + \beta \left( {0,1} \right) \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{x = \alpha }\\{y = \beta }\end{array}} \right. \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{\alpha = x}\\{\beta = y}\end{array}} \right.\] Ahora aplicamos la transformación lineal sobre ese vector genérico, y resolvemos para llegar a una expresión analítica de la transformación lineal: \[F\left( {\left( {x,y} \right)} \right) = F\left( {\alpha \left( {1,0} \right) + \beta \left( {0,1} \right)} \right)\] \[F\left( {\left( {x,y} \right)} \right) = \alpha .F\left( {\left( {1,0} \right)} \right) + \beta .F\left( {\left( {0,1} \right)} \right)\] \[F\left( {\left( {x,y} \right)} \right) = x.\left( {1,0} \right) + y.\left( {\frac{1}{2};1} \right)\] \[F\left( {\left( {x,y} \right)} \right) = \left( {x,0} \right) + \left( {\frac{1}{2}y;y} \right)\] \[F\left( {\left( {x,y} \right)} \right) = \left( {\frac{1}{2}y + x;y} \right)\] En el siguiente archivo de GeoGebra se puede ver el triángulo original, y el transformado. También se puede redefinir la ubicación de los puntos del triángulo original y ver cómo quedaría el transformado en cada caso.
Ejemplo 3
Halle la expresión analítica de cada una de las siguientes transformaciones \(\left( {{\mathbb{R}^2} \to {\mathbb{R}^2}} \right)\):
a) Simetría respecto de la recta \(y = 3x\)
Resolución
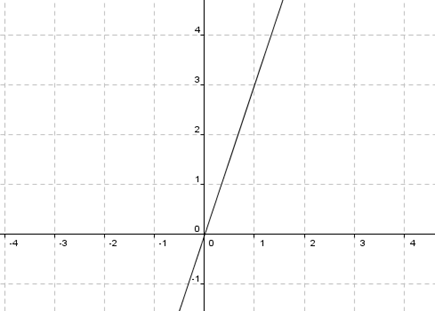
La clave para resolver este ejercicio es elegir una base conveniente para definir la simetría. Grafiquemos la recta \(y = 3x\):
Primero hay que entender qué significa una reflexión respecto de una recta. Supongamos que nos piden una simetría respecto del eje \(x\). Si tenemos un cuadrado así como el rojo, se transforma en un cuadrado como el violeta:
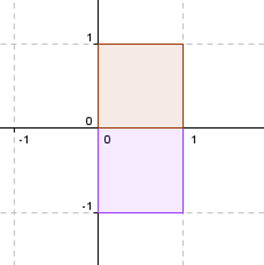
Todos los puntos que pertenecen al eje \(x\) quedan idénticos. Y los puntos que están sobre el eje \(y\) se transforman en su opuesto. Entonces: \[\left\{ {\begin{array}{*{20}{c}}{F\left( {\left( {1,0} \right)} \right) = \left( {1,0} \right)}\\{F\left( {\left( {0,1} \right)} \right) = \left( {0, – 1} \right)}\end{array}} \right.\] Considerando estas ideas sobre simetría, en nuestro caso tomamos un vector que esté sobre el eje de simetría y otro perpendicular a él:
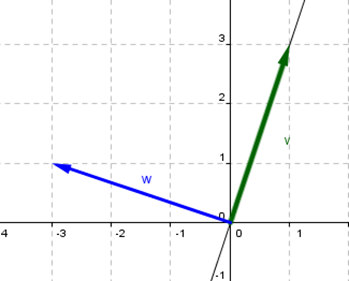
\[v = \left( {1,3} \right){\rm{\;}},{\rm{\;}}w = \left( { – 3,1} \right)\] ¿Cuál es el transformado del vector \(\left( {1,3} \right)\) que está sobre el eje de simetría? ¿Cuál es el transformado del vector \(\left( { – 3,1} \right)\) que es perpendicular al eje de simetría? Entonces: \[\left\{ {\begin{array}{*{20}{c}}{F\left( {\left( {1,3} \right)} \right) = \left( {1,3} \right)\;\;\;\;\;\;\;\;\;\;\;\;porque\;está \;sobre\;el\;eje\;de\;simetría}\\{F\left( {\left( { – 3,1} \right)} \right) = \left( {3, – 1} \right)\;\;\;\;\;porque\;es\;perpendicular\;al\;eje\;de\;simetría}\end{array}} \right.\] Ahora queda el problema técnico de buscar la fórmula de esta transformación lineal: \[\left( {x,y} \right) = \alpha \left( {1,3} \right) + \beta \left( { – 3,1} \right) \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x = \alpha – 3\beta }\\{y = 3\alpha + \beta }\end{array} \Rightarrow \beta = \frac{{y – 3x}}{{10}} \wedge {\rm{\;}}\alpha = \frac{{x + 3y}}{{10}}} \right.\] Aplico \(F\) a ambos miembros \[F\left( {\left( {x,y} \right)} \right) = F\left( {\alpha \left( {1,3} \right) + \beta \left( { – 3,1} \right)} \right)\] Como \(F\) es transformación lineal: \[F\left( {\left( {x,y} \right)} \right) = \alpha .F\left( {\left( {1,3} \right)} \right) + \beta F\left( {\left( { – 3,1} \right)} \right)\] \[F\left( {\left( {x,y} \right)} \right) = \left( {\frac{{x + 3y}}{{10}}} \right).\left( {1,3} \right) + \left( {\frac{{y – 3x}}{{10}}} \right)\left( {3, – 1} \right)\] \[F\left( {\left( {x,y} \right)} \right) = \left( {\frac{{x + 3y}}{{10}},{\rm{\;}}\frac{{3x + 9y}}{{10}}} \right) + \left( {\frac{{3y – 9x}}{{10}},\frac{{ – y + 3x}}{{10}}} \right)\] \[F\left( {\left( {x,y} \right)} \right) = \left( {\frac{{6y – 8x}}{{10}},\frac{{6x + 8y}}{{10}}} \right)\] \[F\left( {\left( {x,y} \right)} \right) = \left( {\frac{{3y – 4x}}{5},\frac{{3x + 4y}}{5}} \right)\] Podemos ver en GeoGebra cómo opera la transformación:
Ejemplo 4
El propósito de este ejercicio es destacar cuándo es posible aplicar el teorema fundamental de las transformaciones lineales. Sugerimos una lectura cuidadosa de cada uno de los casos presentados a continuación: Analizar si existe y es única la transformación lineal \(T:{\mathbb{R}^3} \to {\mathbb{R}^3}\) que verifica:
Caso A \[\left\{ {\begin{array}{*{20}{c}}{T\left( {\left( {1,0,0} \right)} \right) = \left( {0,1,0} \right)}\\{T\left( {\left( {0,1,0} \right)} \right) = \left( {0,1,0} \right)}\\{T\left( {\left( {1,1,1} \right)} \right) = \left( {0,0,0} \right)}\end{array}} \right.\]
Caso B \[\left\{ {\begin{array}{*{20}{c}}{T\left( {\left( {1,0,0} \right)} \right) = \left( {0,1,0} \right)}\\{T\left( {\left( {0,1,0} \right)} \right) = \left( {0,1,0} \right)}\\{T\left( {\left( {1, – 1,0} \right)} \right) = \left( {1,0,0} \right)}\end{array}} \right.\]
Caso C \[\left\{ {\begin{array}{*{20}{c}}{T\left( {\left( {1,0,0} \right)} \right) = \left( {0,1,0} \right)}\\{T\left( {\left( {0,1,0} \right)} \right) = \left( {0,1,0} \right)}\\{T\left( {\left( {1, – 1,0} \right)} \right) = \left( {0,0,0} \right)}\end{array}} \right.\]
Resolución
¿Cuál es la hipótesis del teorema? O sea, ¿qué debe cumplirse para que el teorema tenga validez?
Los vectores del dominio deben ser una base, es decir que debemos prestar atención en cada caso a los vectores señalados:
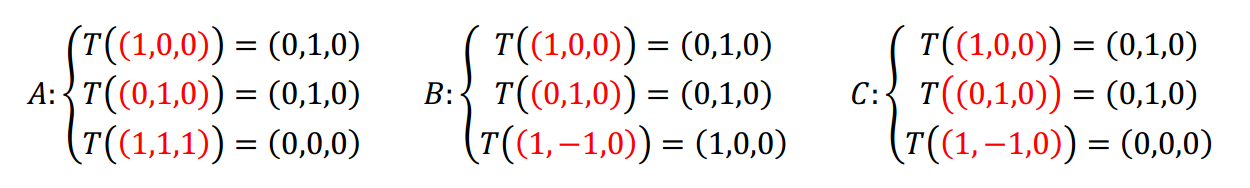
Caso A
En el caso A los tres vectores son base de \({\mathbb{R}^3}\) y entonces podemos aplicar el Teorema Fundamental de las Transformaciones Lineales. Como lo establece el teorema, se puede afirmar que existe una única transformación lineal que verifica las condiciones dadas. ¿Cuál es el mecanismo para buscar la fórmula? Consideramos un vector \(\left( {x,y,z} \right)\) y buscamos sus coordenadas respecto de la base de partida: \[\left( {x.y,z} \right) = \alpha \left( {1,0,0} \right) + \beta \left( {0,1,0} \right) + \gamma \left( {1,1,1} \right)\] \[\left\{ {\begin{array}{*{20}{c}}{x = \alpha + \gamma }\\{y = \beta + \gamma }\\{z = \gamma }\end{array}} \right.{\rm{\;\;}} \Rightarrow {\rm{\;}}\left\{ {\begin{array}{*{20}{c}}{\alpha = x – z}\\{\beta = y – z}\\{\gamma = z}\end{array}} \right.\] Aplicamos la transformación lineal a ambos miembros: \[T\left( {\left( {x,y,z} \right)} \right) = \alpha T\left( {\left( {1,0,0} \right)} \right) + \beta T\left( {\left( {0,1,0} \right)} \right) + \gamma T\left( {\left( {1,1,1} \right)} \right)\] Y ahora sustituimos las coordenadas obtenidas: \[T\left( {\left( {x,y,z} \right)} \right) = \left( {x – z} \right)\left( {0,1,0} \right) + \left( {y – z} \right)\left( {0,1,0} \right) + \left( z \right)\left( {0,0,0} \right)\] \[T\left( {\left( {x,y,z} \right)} \right) = \left( {0,x – z,0} \right) + \left( {0,y – z,0} \right) = \left( {0,x + y – 2z,0} \right)\] \[T\left( {\left( {x,y,z} \right)} \right) = \left( {0,x + y – 2z,0} \right)\]
Caso B
En el caso B, el conjunto de vectores de partida es linealmente dependiente, no es base de \({\mathbb{R}^3}\). Si no se cumplen las hipótesis de un teorema, éste no puede aplicarse. ¿Cómo podemos determinar si existe una transformación lineal que verifique estas condiciones?
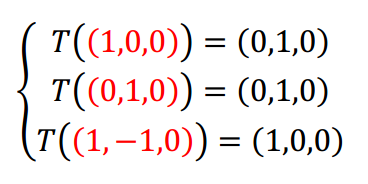
Lo que define a una transformación lineal es la conservación de las combinaciones lineales. ¡Esto es lo que debemos controlar! Veamos la diferencia entre el caso B y el C: Observamos que el tercer vector se puede obtener como combinación lineal de los primeros dos: \[\left( {1, – 1,0} \right) = \left( {1,0,0} \right) – \left( {0,1,0} \right)\] Entonces entre sus transformados debería cumplirse la misma relación:
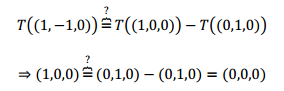
No se conserva la combinación lineal, entonces no existe una transformación lineal que cumpla las condiciones dadas.
Caso C
En el caso C tenemos la siguiente información:
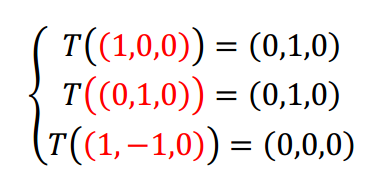
Tampoco se puede aplicar el TFTL, porque el conjunto de vectores de partida es linealmente dependiente. Igualmente podemos preguntarnos: ¿Se conserva la combinación lineal? Notemos que el tercer vector es la diferencia del primero con el segundo: \[\left( {1, – 1,0} \right) = \left( {1,0,0} \right) – \left( {0,1,0} \right)\] Aplicamos la transformación lineal suponiendo que se conservan las combinaciones lineales:
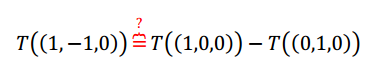
Reemplazando:
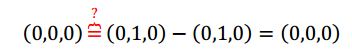
Lo cual es verdadero. Entonces podemos concluir que existe la transformación lineal aunque no quede unívocamente determinada por la información disponible. Para definir una TL bastaría con establecer cuáll es el transformado de un tercer vector LI con \(\left( {1,0,0} \right)\) y \(\left( {0,1,0} \right)\). Agreguemos un dato nuevo para que quede bien definida: \[T\left( {\left( {0,0,1} \right)} \right) = \left( {0,0,1} \right)\] ¿Existe una TL que cumpla con las condiciones iniciales más ésta que acabamos de agregar? Llamemos: \[\left\{ {\begin{array}{*{20}{c}}{{T_1}\left( {\left( {1,0,0} \right)} \right) = \left( {0,1,0} \right)}\\{{T_1}\left( {\left( {0,1,0} \right)} \right) = \left( {0,1,0} \right)}\\{{T_1}\left( {\left( {0,0,1} \right)} \right) = \left( {0,0,1} \right)}\end{array}} \right.\] Ahora \({T_1}\) queda bien definida y podríamos hallar su fórmula. ¿Cómo podrían definir una transformación \({T_2}\) distinta de \({T_1}\) que también cumpla con las condiciones iniciales? Resumamos lo que obtuvimos analizando estos tres casos:
- Caso A: La transformación lineal existe y es única.
- Caso B: No existe, no se conservan las combinaciones lineales.
- Caso C: Existe pero no es única, no podemos encontrar una fórmula porque la transformación lineal no quedó definida.
Ejemplo 5
Halle la expresión analítica de cada una de las siguientes transformaciones \({\mathbb{R}^3} \to {\mathbb{R}^3}\):
a) Reflexión respecto del plano \(x = y\)
Resolución
Este ejercicio requiere elegir una buena base. Una gráfica del plano \(x = y\) se puede ver a continuación:
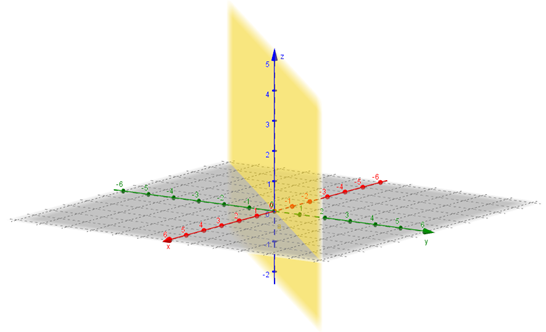
El arte para resolver este ejercicio es elegir tres vectores linealmente independientes que sepamos en qué se transforman. ¿Cuál es el simétrico de un vector que esté sobre el plano? El mismo vector. Entonces podemos elegir dos vectores no paralelos incluidos en el plano: \[T\left( {{v_1}} \right) = {v_1}\] \[T\left( {{v_2}} \right) = {v_2}\] ¿Y si tomamos un vector perpendicular al plano, digamos \({v_3}\), en que se transforma? \[T\left( {{v_3}} \right) = – {v_3}\] Ahora debemos elegir \({v_1}\), \({v_2}\) y \({v_3}\) de acuerdo con el plano dado. Proponemos: \[{v_1} = \left( {1,1,0} \right)\] \[{v_2} = \left( {0,0,1} \right)\] \[{v_3} = \left( {1, – 1,0} \right)\] Donde los vectores \({v_1}\) y \({v_2}\) están en el plano y el vector \({v_3}\) es perpendicular al plano. De esta forma sabemos cómo se transforman: \[\left\{ {\begin{array}{*{20}{c}}{T\left( {\left( {1,1,0} \right)} \right) = \left( {1,1,0} \right)}\\{T\left( {\left( {0,0,1} \right)} \right) = \left( {0,0,1} \right)}\\{T\left( {\left( {1, – 1,0} \right)} \right) = \left( { – 1,1,0} \right)}\end{array}} \right.\] Ya queda definida la transformación lineal sobre una base del dominio. Dejamos a cargo del lector encontrar la fórmula de la TL. Les proponemos que definan la TL sobre otra base con las mismas características: dos vectores del plano y uno perpendicular a él. Luego busquen la expresión analítica, ¿coincide con la anterior? Los vectores no son únicos: \({v_1}\) y \({v_2}\) son dos vectores cualesquiera (LI) del plano y \({v_3}\) es un vector perpendicular cualquiera. No importa cuáles elijamos, obtendremos la misma transformación lineal.
Ejercicio para el lector 2
Definir una transformación lineal \(F\) de \({\mathbb{R}^3} \to {\mathbb{R}^{2 \times 2}}\) que verifique las dos condiciones que siguen:
i) \(Nu\left( F \right)\; = \;gen\;\left\{ {\;\left( {1,1,0} \right)\;} \right\}\)
ii) \(Im\left( F \right) \subseteq \;S = \left\{ {\;A \in {\mathbb{R}^{2×2}}\;:\;\;A = {A^t}\;} \right\}\)
Obtener la fórmula de la transformación definida.
Observación: este ejercicio no es de respuesta única.

