Conceptos básicos
Definición de Matriz
Una matriz \(A\) de \(m \times n\) es un ordenamiento rectangular de escalares dispuestos en \(m\) filas y \(n\) columnas. Para designar a cada uno de los \(m.n\) elementos de la matriz se utiliza un doble subíndice que indica el número de fila y número de columna que le corresponde en el arreglo: \[A = \left( {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}& \cdots &{{a_{1n}}}\\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}& \cdots &{{a_{2n}}}\\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}& \cdots &{{a_{3n}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\{{a_{m1}}}&{{a_{m2}}}&{{a_{m3}}}& \cdots &{{a_{mn}}}\end{array}} \right)\] Así, \(\;{a_{34}}\) es el elemento ubicado en la fila tres y la columna cuatro y en general \({a_{ij}}\) es el elemento de la matriz \(A\) que está en la fila \(i\) y en la columna \(j\).
Las matrices suelen designarse con letras mayúsculas: se anota \(A \in {\mathbb{R}^{mxn}}\) para indicar que es una matriz con \(m\) filas y \(n\) columnas cuyos elementos son números reales. Se indican con paréntesis o con corchetes:
Por ejemplo una matriz de dos filas y tres columnas se puede escribir así: \[A = \left( {\begin{array}{*{20}{c}}3&2&{0\;}\\{ – 2}&{4\;}&1\end{array}} \right)\;\;\;\;\;,\;\;\;\;\;\;A \in {\mathbb{R}^{2 \times 3}}\]
En este caso, diremos que el tamaño u orden de \(A\) es \(2 \times 3\).
Matriz columna
Podemos pensar los vectores como casos particulares de matrices: \[C = \left( {\begin{array}{*{20}{c}}2\\{\begin{array}{*{20}{c}}0\\1\end{array}}\end{array}} \right)\;\;matriz\;o\;vector\;columna\;\;,\;\;\;C \in {\mathbb{R}^{3 \times 1}}\]
Matriz fila
O también: \[F = \left( {2\;\;\;\;\;0\;\;\;\;\;1} \right)\;\;\;matriz\;o\;vector\;fila\;\;\;,\;\;\;\;F \in {\mathbb{R}^{1 \times 3}}\]
Matriz nula
La matriz nula es aquélla cuyos elementos son todos ceros. La simbolizamos con \(O\). (En la guía de trabajos prácticos se la designa como \(N\))
Igualdad de matrices
Dos matrices son iguales si son del mismo orden (tamaño) y sus elementos respectivos son iguales. \[A,B \in {\mathbb{R}^{mxn}}\;\;\;\;\;A = B\; \Leftrightarrow \;{a_{ij}} = {b_{ij}}\;\;\forall i,j\]
Operaciones con matrices
Suma de matrices
Sean \(A,B \in {\mathbb{R}^{m \times n}}\) entonces: \[A + B = C \in {\mathbb{R}^{m \times n}}\;\;|\;\;\;{c_{ij}} = {a_{ij}} + {b_{ij}}\;\;\;\forall i,j\]
Ejemplo
Sean: \[A = \left( {\begin{array}{*{20}{c}}0&{ – 1}&1\\{ – 2}&3&2\end{array}} \right)\;\;,\;\;B = \left( {\begin{array}{*{20}{c}}1&0&{ – 3}\\3&{ – 1}&2\end{array}} \right)\;\;\;\] Entonces la suma es: \[A + B = \left( {\begin{array}{*{20}{c}}0&{ – 1}&1\\{ – 2}&3&2\end{array}} \right) + \left( {\begin{array}{*{20}{c}}1&0&{ – 3}\\3&{ – 1}&2\end{array}} \right) = \left( {\begin{array}{*{20}{c}}1&{ – 1}&{ – 2}\\1&2&4\end{array}} \right)\]
Producto de un escalar por una matriz
Sean \(A \in {\mathbb{R}^{m \times n}},\;k \in \mathbb{R}\), entonces: \[kA = B\; \in {\mathbb{R}^{m \times n}}\;\;|\;\;\;{b_{ij}} = k{a_{ij}}\;\;\;\forall i,j\;\] Por ejemplo, si \(A = \left( {\begin{array}{*{20}{c}}0&{ – 1}&1\\{ – 2}&3&2\end{array}} \right)\) , entonces \(3A = \left( {\begin{array}{*{20}{c}}0&{ – 3}&3\\{ – 6}&9&6\end{array}} \right)\) Cuando \(k\; = \; – 1\), obtenemos la matriz opuesta de A: \[ – A = \left( { – 1} \right)A = \left( {\begin{array}{*{20}{c}}0&1&{ – 1}\\2&{ – 3}&{ – 2}\end{array}} \right)\] Podemos así definir la diferencia (resta) entre dos matrices del mismo tamaño: \[A – B = A + \left( { – B} \right)\] O sea: \[A – B = C \in {\mathbb{R}^{m \times n}}\;\;\;\;|\;\;\;{c_{ij}} = {a_{ij}} – {b_{ij}}\]
Ejemplo
Sean las matrices: \[A = \left( {\begin{array}{*{20}{c}}3&2\\1&{ – 1}\\4&5\end{array}} \right)\;\;\;,\;\;\;B = \left( {\begin{array}{*{20}{c}}0&2\\4&{ – 1}\\5&3\end{array}} \right)\] Entonces: \[2A – B = \left( {\begin{array}{*{20}{c}}6&4\\2&{ – 2}\\8&{10}\end{array}} \right) – \left( {\begin{array}{*{20}{c}}0&2\\4&{ – 1}\\5&3\end{array}} \right) = \left( {\begin{array}{*{20}{c}}6&2\\{ – 2}&{ – 1}\\3&7\end{array}} \right)\]
Ejemplo
Hallar \(X,Y \in {\mathbb{R}^{2 \times 2}}\) tales que: \[2X – Y = \left( {\begin{array}{*{20}{c}}1&0\\0&4\end{array}} \right)\;\;\;\;\;\;\;\;\;\;\;\;\left[ 1 \right]\] \[3X + Y = \left( {\begin{array}{*{20}{c}}4&5\\0&1\end{array}} \right)\;\;\;\;\;\;\;\;\;\;\;\;\left[ 2 \right]\;\]
Resolución
Es un sistema de ecuaciones matricial. Las incógnitas son matrices. Podríamos plantear el sistema escribiendo las matrices como \[X = \left( {\begin{array}{*{20}{c}}{{x_1}}&{{x_2}}\\{{x_3}}&{{x_4}}\end{array}} \right)\;\;\;,\;\;\;Y = \left( {\begin{array}{*{20}{c}}{{y_1}}&{{y_2}}\\{{y_3}}&{{y_4}}\end{array}} \right)\] Pero quedarían 8 ecuaciones con 8 incógnitas. Para facilitar la resolución, podemos recurrir a las herramientas que utilizamos para resolver sistemas de ecuaciones lineales. Si sumamos miembro a miembro las ecuaciones queda: \[5X = \left( {\begin{array}{*{20}{c}}1&0\\0&4\end{array}} \right) + \left( {\begin{array}{*{20}{c}}4&5\\0&1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}5&5\\0&5\end{array}} \right)\] \[ \Rightarrow X = \left( {\begin{array}{*{20}{c}}1&1\\0&1\end{array}} \right)\] Reemplazando en \(\left[ 1 \right]\) \[\left( {\begin{array}{*{20}{c}}2&2\\0&2\end{array}} \right) – Y = \left( {\begin{array}{*{20}{c}}1&0\\0&4\end{array}} \right)\;\; \Rightarrow \;\;Y = \left( {\begin{array}{*{20}{c}}1&2\\0&{ – 2}\end{array}} \right)\] Sugerimos al lector que verifique los resultados obtenidos reemplazando en [2].
Propiedades de la suma de matrices y del producto por un escalar
Sean \(A,B,C \in {\mathbb{R}^{mxn}}\;\;y\;\;\alpha ,\;\beta \in \mathbb{R}\). Vimos que: \(A + B \in {\mathbb{R}^{mxn}}\) y \(\alpha A \in {\mathbb{R}^{mxn}}\). Estas operaciones verifican las siguientes propiedades:
- \(A + B = B + A\;\;\;\;\)
- \(\left( {A + B} \right) + C = A + \left( {B + C} \right)\;\;\;\;\)
- \(A + O = O + A = A\;\;\;\;\;\)
- \(A + \left( { – A} \right) = \left( { – A} \right) + A = O\)
- \(\alpha \left( {A + B} \right) = \alpha A + \alpha B\)
- \(\left( {\alpha + \beta } \right)A = \alpha A + \beta A\)
- \(\alpha \left( {\beta A} \right) = \left( {\alpha \beta } \right)A\)
- \(1A = A\)
Puede observarse la analogía entre estas propiedades y las que habíamos enunciado en la unidad anterior para vectores de \({\mathbb{R}^3}\).
Producto de matrices
Intuitivamente podría pensarse que el producto de matrices se obtiene multiplicando los elementos correspondientes. Sin embargo, esta definición no resulta útil para resolver problemas que involucren matrices. La experiencia matemática vinculada sobre todo a los sistemas de ecuaciones lineales, ha motivado la siguiente definición de producto de matrices. Definiremos primero el producto de una matriz fila por una matriz columna, y luego generalizaremos. \[{\rm{Si}}\;\;\;A = \left( {{a_1}\;\;\;{a_2}\; \cdots \;\;\;{a_n}} \right)\; \in {\mathbb{R}^{1 \times n}}\;\;\;{\rm{\;y}}\;\;\;\;B = \left( {\begin{array}{*{20}{c}}{{b_1}}\\{\begin{array}{*{20}{c}}{{b_2}}\\ \vdots \\{{b_n}}\end{array}}\end{array}} \right)\; \in {\mathbb{R}^{nx1}}\;,\;{\rm{entonces}}:\;\;\;\;\] \[AB = \left( {{a_1}\;\;\;{a_2}\; \cdots \;\;\;{a_n}} \right)\left( {\begin{array}{*{20}{c}}{{b_1}}\\{\begin{array}{*{20}{c}}{{b_2}}\\ \vdots \\{{b_n}}\end{array}}\end{array}} \right) = {a_1}{b_1} + {a_2}{b_2} + \cdots + {a_n}{b_n}\] Observemos la similitud con el producto escalar de vectores. Sean \(A \in {\mathbb{R}^{m \times n}}\) y \(B \in {\mathbb{R}^{n \times p}}\), o sea se cumple que la cantidad de columnas de la primera matriz es igual a la cantidad de filas de la segunda:
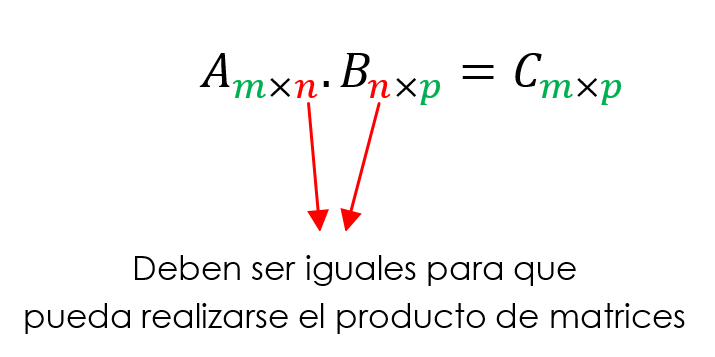
Entonces el producto es:
![]()
Una forma alternativa de expresar el producto es: \[AB = C \in {\mathbb{R}^{m \times p}}\;\;\;|\;\;\;\;\;{c_{ij}} = \mathop \sum \limits_{k = 1}^n {a_{ik}}\;{b_{kj}}\]
Ejemplo
Sean, \[A = \left( {\begin{array}{*{20}{c}}1&2&3\\4&1&0\end{array}} \right)\;\;\;,\;\;\;\;B = \left( {\begin{array}{*{20}{c}}1&1&2\\1&{ – 1}&0\\2&0&3\end{array}} \right)\;\;\;\;\;A \in {\mathbb{R}^{2 \times 3}}\;\;\;\;B \in {\mathbb{R}^{3 \times 3}}\;\;\] Es posible calcular \(A.B\) porque \(A\) tiene tres columnas y \(B\) tiene tres filas. El resultado del producto es una matriz de \(2 \times 3.\)
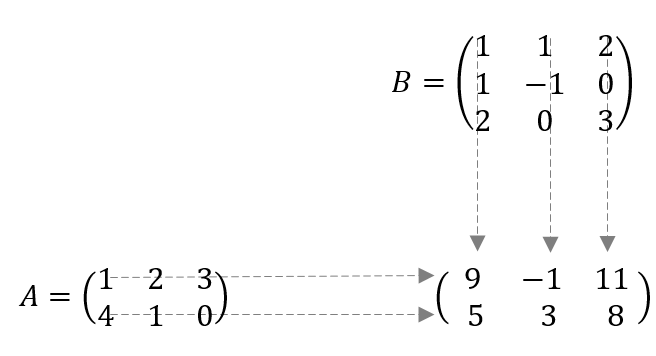
\[AB = \left( {\begin{array}{*{20}{c}}{1.1 + 2.1 + 3.2}&{1.1 + 2.\left( { – 1} \right) + 3.0}&{1.2 + 2.0 + 3.3}\\{4.1 + 1.1 + 0.2}&{4.1 + 1.\left( { – 1} \right) + 0.0}&{4.2 + 1.0 + 0.3}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}9&{ – 1}&{11}\\5&3&8\end{array}} \right)\] No se puede calcular \(BA\) porque el número de columnas de \(B\) no coincide con el número de filas de \(A\).
Ejemplo
\[P = \left( {\begin{array}{*{20}{c}}1&1\\2&1\\3&0\end{array}} \right)\;\;,\;\;\;\;Q = \left( {\begin{array}{*{20}{c}}3&2&1\\1&3&{ – 1}\end{array}} \right)\] \[PQ \in {\mathbb{R}^{3 \times 3}}\;\;,\;\;\;PQ = \left( {\begin{array}{*{20}{c}}4&5&0\\7&7&1\\9&6&3\end{array}} \right)\] \[QP \in {\mathbb{R}^{2 \times 2}}\;\;\;,\;\;\;QP = \left( {\begin{array}{*{20}{c}}{10}&5\\4&4\end{array}} \right)\] O sea que el producto de matrices no es conmutativo.
Propiedades del producto
En lo que sigue entendemos que las operaciones mencionadas pueden efectuarse.
1) \(\left( {AB} \right)C = A\left( {BC} \right)\) asociatividad
2) \(\left( {A + B} \right)\;C = AC + BC\) distributividad a derecha
\(P\left( {Q + R} \right) = PQ + PR\) distributivida a izquierda
3) \(\left( {kA} \right)B = k\left( {AB} \right) = A\left( {kB} \right)\;\;,\;\;k \in \mathbb{R}\)
4) \(OA = O\;\;\;\;y\;\;\;AO = O\;,\;\;\) siendo \(O\) la matriz nula
Ejercicio para el lector 1
Sean \(A \in {\mathbb{R}^{m \times n}}\;,\;\;\;B,C \in {\mathbb{R}^{n \times p}}\) Analizar la validez de cada una de las siguientes proposiciones:
- \(AB = 0 \Rightarrow A = 0 \vee B = 0\)
- \(AB = AC \wedge A \ne 0 \Rightarrow B = C\)
Ejercicio para el lector 2
Un comercio que vende productos de electrónica, paga una comisión a los vendedores y tiene un beneficio (ganancia) según cada producto. En una tabla se registra el precio de venta, el beneficio para el comercio, la comisión para el vendedor y el costo del producto. Además se tiene información sobre las unidades vendidas en diferentes sucursales. A continuación mostramos dos tablas que resumen esa información para el mes de agosto 2013:
| Precio de venta, beneficio, costo, comisión por producto [AGOSTO 2013] | |||||
| LED 32′ BA455 | LED BX567 | Smartphone | Tablet 10′ | Notebook | |
| Costo | $ 3.200,00 | $ 4.500,00 | $ 2.500,00 | $ 4.800,00 | $ 5.600,00 |
| Comisión | $ 200,00 | $ 250,00 | $ 30,00 | $ 40,00 | $ 120,00 |
| Beneficio | $ 700,00 | $ 900,00 | $ 200,00 | $ 340,00 | $ 800,00 |
| Precio de venta | $ 4.100,00 | $ 5.650,00 | $ 2.730,00 | $ 5.180,00 | $ 6.520,00 |
| Unidades vendidas de cada producto por sucursal [AGOSTO 2013] | ||||
| Sucursal 1 | Sucursal 2 | Sucursal 3 | Sucursal 4 | |
| LED 32′ BA455 | 23 | 67 | 43 | 4 |
| LED BX567 | 56 | 20 | 32 | 43 |
| Smartphone | 10 | 65 | 67 | 65 |
| Tablet 10′ | 45 | 3 | 23 | 76 |
| Notebook | 67 | 65 | 43 | 80 |
Si \(A\) y \(B\) son las matrices correspondientes a estas tablas: a) Calcular e interpretar el producto \(AB\). ¿Cuál es la sucursal que obtuvo la máxima ganancia? b) ¿Se puede calcular \(BA\)? ¿Tiene interpretación práctica \(BA\)? Nota: hacer el producto de matrices de órdenes grandes puede implicar demasiado trabajo de cálculo. En estos casos se puede utilizar la ayuda de calculadoras o de un software. En el siguiente link hay un tutorial para hacer cálculos entre matrices con wxMaxima. (Descarga de wxMaxima)
Traspuesta de una matriz
La traspuesta de una matriz \(A \in {\mathbb{R}^{m \times n}}\), que indicamos como \({A^t}\), es la matriz de \(n \times m\) que se obtiene a partir de \(A\) cambiando las filas por las columnas.
Ejemplo
Si \(A = \left( {\begin{array}{*{20}{c}}1&2&3\\4&5&6\end{array}} \right)\) \( \in {\mathbb{R}^{2×3}}\) , entonces su traspuesta es: \({A^t} = \left( {\begin{array}{*{20}{c}}1&4\\2&5\\3&6\end{array}} \right)\;\) \( \in {\mathbb{R}^{3×2}}\)
Propiedades de la trasposición
1) \({\left( {A + B} \right)^t} = {A^t} + {B^t}\)
2) \({\left( {kA} \right)^t} = k{A^t},\;\;k \in \mathbb{R}\)
3) \({\left( {{A^t}} \right)^t} = A\)
4) \({\left( {AB} \right)^t} = {B^t}{A^t}\)
Ejemplo
Sean \(A = \left( {\begin{array}{*{20}{c}}1&2&3\\4&5&6\end{array}} \right)\;\;\;\;\;\;,\;\;\;\;\;\;B = \left( {\begin{array}{*{20}{c}}1&1&0\\0&1&{ – 1}\\1&2&1\end{array}} \right)\)
Calculemos:
a) \({\left( {AB} \right)^t}\)
b) \({A^t}{B^t}\)
c) \({B^t}{A^t}\)
Resolución
Ítem a
Calculamos \(AB\) y luego trasponemos:
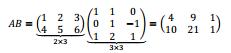
\[{\left( {AB} \right)^t} = \left( {\begin{array}{*{20}{c}}4&{10}\\9&{21}\\1&1\end{array}} \right)\]
Ítem b
Trasponemos y luego hacemos el producto:
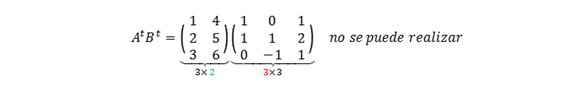
Como no coinciden el número de columnas de \({A^t}\) con el número de filas de \({B^t}\), no se puede hacer el producto.
Ítem c
\[{B^t}{A^t} = \left( {\begin{array}{*{20}{c}}1&0&1\\1&1&2\\0&{ – 1}&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}1&4\\2&5\\3&6\end{array}} \right) = \left( {\begin{array}{*{20}{c}}4&{10}\\9&{21}\\1&1\end{array}} \right)\]
En este ejemplo verificamos la propiedad enunciada: \({\left( {AB} \right)^t}\) = \({B^t}{A^t}\)
Matrices cuadradas
Una matriz cuadrada es aquélla que tiene igual número de filas y de columnas. Denominamos \({\mathbb{R}^{nxn}}\) al conjunto de matrices cuadradas de orden n (n filas y n columnas).
La diagonal principal de una matriz cuadrada está formada por los elementos \({a_{ii}}\).
Matriz identidad
La matriz identidad, que simbolizamos con \(I\), es una matriz cuadrada con unos en la diagonal principal y ceros en todos los demás elementos. \[{I_2} = \left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right)\] \[{I_3} = \left( {\begin{array}{*{20}{c}}1&0&0\\0&1&0\\0&0&1\end{array}} \right)\] \[{I_n} = \left( {\begin{array}{*{20}{c}}1&0&0& \cdots &0\\0&1&0& \cdots &0\\0&0&1& \cdots &0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\0&0&0& \cdots &1\end{array}} \right)\]
Propiedad: La matriz identidad es el elemento neutro para el producto de matrices cuadradas. Se comporta como el 1 para los números reales.
Lo mostramos para matrices \(2 \times 2\):
\[\left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right)\left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right) = \left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right)\] \[\left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right) = \left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right)\]
\[A.I=I.A=A\]
Matriz inversa
En el conjunto de los números reales existe el inverso multiplicativo para todo número real distinto de cero. Dado un número real \(a\) distinto de cero, \(b\) es su inverso multiplicativo si y solo si \(a.b = 1\).
A continuación definiremos el inverso multiplicativo para matrices cuadradas.
Se dice que \(A \in {\mathbb{R}^{n \times n}}\) es inversible si y sólo si existe una matriz \(B \in {\mathbb{R}^{n \times n}}\) tal que:
\[AB = BA = I\]
Ejemplo
Analizar si las siguientes matrices son inversibles: \[A = \left( {\begin{array}{*{20}{c}}3&1\\{ – 3}&{ – 1}\end{array}} \right)\] \[P = \left( {\begin{array}{*{20}{c}}3&1\\2&1\end{array}} \right)\] ¿\(\exists B \in {\mathbb{R}^{2 \times 2}}\;|\;AB = I\)? \[\left( {\begin{array}{*{20}{c}}3&1\\{ – 3}&{ – 1}\end{array}} \right)\left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right) = \left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right) \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{3a + c = 1}\\{3b + d = 0}\\{ – 3a – c = 0}\\{ – 3b – d = 1}\end{array}} \right.\] \[ \Rightarrow 1 = 0\;Sistema\;incompatible\]
Como llegamos a una contradicción, la matriz \(A\) no es inversible.
Observación: el único número real no inversible es el cero; pero en \({\mathbb{R}^{n \times n}}\) vemos que existen matrices no nulas que no tienen inversa.
Con la matriz \(P\):
¿\(\exists \;Q \in {\mathbb{R}^{2 \times 2}}\;|\;\;PQ = I\)? \[\left( {\begin{array}{*{20}{c}}3&1\\2&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right) = \left( {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right)\; \Rightarrow \;\left\{ {\begin{array}{*{20}{c}}{3a + c = 1}\\{3b + d = 0}\\{2a + c = 0}\\{2b + d = 1}\end{array}} \right.\;\; \Rightarrow \;\;a = 1\;\;,\;\;\;b = – 1\;\;,\;\;\;\;c = – 2\;\;,\;\;\;d = 3\] \[Q = \left( {\begin{array}{*{20}{c}}1&{ – 1}\\{ – 2}&3\end{array}} \right)\]
Les proponemos verificar que \(QP = I\).
Entonces \(P\) es inversible, y \(Q\) se denomina inversa de \(P\).
La notación es:
\[Q = {P^{ – 1}}\]
Entonces:
\[P.P^{-1}=P^{-1}.P=I\]
Más adelante analizaremos qué condición debe cumplir una matriz para ser inversible. Observación: Sean \(A,B \in {\mathbb{R}^{n \times n}}\) entonces: \[AB = I\; \Leftrightarrow \;BA = I\;\;\;\;\;\;\;\;\left[ 1 \right]\] O sea: para matrices cuadradas, si encontramos \(B\) tal que \(AB = I\) , podemos afirmar que \(B\) es la inversa de \(A\).
Propiedades de la inversión de matrices
Sean \(A,B \in {\mathbb{R}^{nxn}}\;\)inversibles Entonces:
1) \(AB\) es inversible y su inversa es: \( \left(AB\right)^{-1}=B^{-1}A^{-1}\)
Esto significa que la inversa de \(AB\) es \({B^{ – 1}}{A^{ – 1}}\).
Para demostrar esta propiedad, veamos que: \(\left( {AB} \right)\left( {{B^{ – 1}}{A^{ – 1}}} \right) = I\)
Como el producto de matrices es asociativo, resulta:
\[\left( {AB} \right)\left( {{B^{ – 1}}{A^{ – 1}}} \right) = A\;\left( {B{B^{ – 1}}} \right)\;{A^{ – 1}} = A\;I\;{A^{ – 1}} = A\;{A^{ – 1}} = I\]
El lector puede comprobar que: \(\left( {{B^{ – 1}}{A^{ – 1}}} \right)\;\left( {AB} \right) = I\)
Hemos demostrado que el producto de matrices inversibles es inversible.
¿Ocurre lo mismo con la suma de matrices inversibles?
2) \({\left( {kA} \right)^{ – 1}} = \frac{1}{{k\;}}\;{A^{ – 1}}\;\;\;\left( {k \ne 0} \right)\)
3) \({\left( {{A^t}} \right)^{ – 1}} = {\left( {{A^{ – 1}}} \right)^t}\)
Dejamos las demostraciones a cargo del lector.
Potencias de una matriz cuadrada
Sea \(A \in {\mathbb{R}^{n \times n}}\).
Es posible definir potencias de \(A\) como sigue:
\[{A^2} = A\;A\]
\[{A^3} = A\;A\;A\]
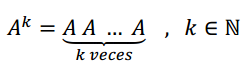
Ejemplo
\[A = \left( {\begin{array}{*{20}{c}}1&2\\3&4\end{array}} \right)\] \[{A^2} = A\;A = \left( {\begin{array}{*{20}{c}}1&2\\3&4\end{array}} \right)\left( {\begin{array}{*{20}{c}}1&2\\3&4\end{array}} \right) = \left( {\begin{array}{*{20}{c}}7&{10}\\{15}&{22}\end{array}} \right)\]
Ejercicio para el lector 3
En una ciudad hay tres empresas de telefonía celular (A, B y C) que controlan el mercado.
Inicialmente cada empresa tiene una fracción de la clientela que denominaremos \({a_0}\), \({b_0}\) y \({c_0}\).
Entonces resulta: \({a_0}\; + \;{b_0}\; + \;{c_0} = 1\) (no hay otras empresas)
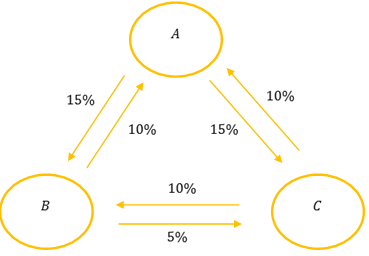
La figura resume el porcentaje de clientes que cambian de empresa durante un período de seis meses.
Este modelo matemático se basa en los siguientes supuestos:
– El porcentaje de cambio entre las empresas se mantiene constante con el tiempo.
– Los clientes seguirán siendo consumidores de una de estas tres empresas.
– No se incorporan nuevos clientes al sistema.
Llamemos \({X_0} = \left( {\begin{array}{*{20}{c}}{{a_0}}\\{{b_0}}\\{{c_0}}\end{array}} \right)\) al vector de estado inicial, y \({X_1} = \left( {\begin{array}{*{20}{c}}{{a_1}}\\{{b_1}}\\{{c_1}}\end{array}} \right)\) al vector que indica la fracción de la clientela que corresponde a cada empresa al cabo de un semestre.
Veamos cómo puede obtenerse \({X_1}\) a partir de \({X_0}\) .
De acuerdo con la figura, podemos deducir que al cabo de un período (semestre) la empresa A conservará 70% de su clientela propia.
¿Qué porcentaje de su clientela conservarán las empresas B y C al cabo de un semestre?
Según los datos, finalizado el 1º semestre la fracción de la clientela que tiene A puede obtenerse así:
\[0,70\;{a_0}\; + \;0,10\;{b_0}\; + \;0,10\;{c_0}\; = \;{a_1}\]
¿Qué ecuaciones permiten obtener \({b_1}\) y \({c_1}\)?
Resulta entonces el siguiente sistema: \[\left\{ {\begin{array}{*{20}{c}}{0,70{a_0} + 0,10{b_0} + 0,10{c_0} = {a_1}}\\{0,15{a_0} + 0,85{b_0} + 0,10{c_0} = {b_1}}\\{0,15{a_0} + 0,05{b_0} + 0,80{c_0} = {c_1}}\end{array}} \right.\]
El lector puede comprobar que este sistema puede expresarse mediante un producto de matrices como sigue:
\[\left( {\begin{array}{*{20}{c}}{0,70}&{0,10}&{0,10}\\{0,15}&{0,85}&{0,10}\\{0,15}&{0,05}&{0,80}\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{a_0}}\\{{b_0}}\\{{c_0}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{{a_1}}\\{{b_1}}\\{{c_1}}\end{array}} \right)\]
O sea: \[M{X_0} = {X_1}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ 1 \right]\]
La matriz \(M \in {\mathbb{R}^{3×3}}\) , que caracteriza la evolución del sistema, se denomina matriz de transición.
¿Qué características presenta esta matriz de transición?
1) Todos sus elementos son números reales comprendidos entre 0 y 1.
2) La suma de los elementos de cada columna es 1.
Las matrices cuadradas que cumplen estas dos condiciones se denominan matrices estocásticas o matrices de probabilidad.
Como la matriz de transición se mantiene para el 2º período, la fracción de clientes para el tiempo \(t\; = \;2\) puede calcularse como:
\[M{X_1} = {X_2}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ 2 \right]\]
De [1] y [2] se deduce que: \(\;{X_2} = {M^2}{X_0}\)
Si los porcentajes de cambio de clientela no cambian en los períodos siguientes, entonces \(M\) no cambia cuando se pasa del estado \((n – 1\)) al estado \(n\).
Por lo tanto:
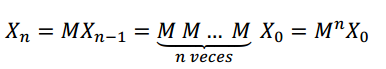
O sea, para obtener cómo se distribuyen los clientes luego de \(n\) períodos, podemos proceder así:
\[X_n=M^nX_0\]
Suponiendo que inicialmente las tres empresas se reparten por partes iguales la clientela, les pedimos que calculen (usando wxMaxima) cómo resulta la distribución de clientes:
- Al cabo de 3 años.
- Al cabo de 10 años
- Al cabo de 15 años
Observen luego de hacer los cálculos que en la medida en que el tiempo pasa, las cuotas de mercado de las empresas tienden a estabilizarse.
4. Responder las mismas preguntas suponiendo que inicialmente las cuotas de mercado de las empresas A, B y C son respectivamente: 0,5 , 0,35 y 0,15.
5. ¿Se produce el mismo fenómeno de estabilización en este caso?
Matrices cuadradas especiales
Matriz simétrica
\(A \in {\mathbb{R}^{n \times n}}\) es simétrica si y sólo si \(A = {A^t}\)
O sea:
\[\;{a_{ij}} = {a_{ji}}\]
Las condiciones para que una matriz de orden tres sea simétrica son:
\[\left\{ {\begin{array}{*{20}{c}}{{a_{21}} = {a_{12}}}\\{{a_{31}} = {a_{13}}}\\{{a_{32}} = {a_{23}}}\end{array}} \right.\]
Entonces la forma de una matriz simétrica de orden tres es: \[A = \left( {\begin{array}{*{20}{c}}a&b&c\\b&d&e\\c&e&f\end{array}} \right)\;\] Por ejemplo \[A = \left( {\begin{array}{*{20}{c}}2&3&1\\3&0&5\\1&5&1\end{array}} \right) = {A^t}\]
Matrices antisimétricas
\(A \in {\mathbb{R}^{n \times n}}\) es antisimétrica si y sólo si \(A = – {A^t}\)
O sea:
\[{a_{ij}} = – {a_{ji}}\]
Veamos qué pasa con los elementos de la diagonal principal.
Si\(\;\;i = j\) debería ser\(\;\;{a_{ii}} = – {a_{ii}}\) , pero el único número que es el opuesto de sí mismo es el cero. Por lo tanto, la diagonal principal está formada por ceros.
Las condiciones para que una matriz de orden tres sea antisimétrica son:
\[\left\{ {\begin{array}{*{20}{c}}{{a_{11}} = {a_{22}} = {a_{33}} = 0}\\{{a_{21}} = – {a_{12}}}\\{{a_{31}} = – {a_{13}}}\\{{a_{32}} = – {a_{23}}}\end{array}} \right.\]
Entonces la forma de una matriz antisimétrica de orden tres es:
\[A = \left( {\begin{array}{*{20}{c}}0&a&b\\{ – a}&0&c\\{ – b}&{ – c}&0\end{array}} \right)\]
Por ejemplo:
\[A = \left( {\begin{array}{*{20}{c}}0&{ – 3}&4\\3&0&0\\{ – 4}&0&0\end{array}} \right) = – {A^t}\]
Ejercicio para el lector 4
Sea \(A \in {\mathbb{R}^{n \times n}}\)
- Probar que \(A + {A^t}\) es simétrica
- Probar que \(A – {A^t}\) es antisimétrica
Observemos que:
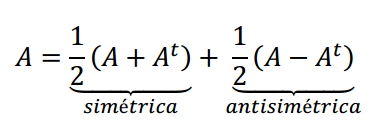
Entonces: toda matriz cuadrada puede expresarse como la suma de una simétrica y una antisimétrica.
¿Cómo se expresa \(\;A = \left( {\begin{array}{*{20}{c}}3&{ – 4}\\8&2\end{array}} \right)\) como suma de una matriz simétrica y una antisimétrica?
Matrices triangulares
\(A \in {\mathbb{R}^{n \times n}}\) es una matriz triangular superior cuando los elementos debajo de la diagonal principal son ceros: \[A = \left( {\begin{array}{*{20}{c}}a&b&c\\0&d&e\\0&0&f\end{array}} \right)\] \[{\rm{Si}}\;i > j \Rightarrow {a_{ij}} = 0\] \(B \in {\mathbb{R}^{n \times n}}\) es una matriz triangular inferior cuando los elementos por encima de la diagonal principal son ceros: \[B = \left( {\begin{array}{*{20}{c}}a&0&0\\b&c&0\\d&e&f\end{array}} \right)\] \[{\rm{Si}}\;i < j \Rightarrow {a_{ij}} = 0\]
Matrices diagonales
Una matriz \(D\) es diagonal si es triangular superior e inferior:
\(D \in {\mathbb{R}^{n \times n}}\) diagonal \( \Leftrightarrow \;\;{a_{ij}} = 0\;\;\;\forall i \ne j\)
La forma de una matriz diagonal de orden tres es: \[D = \left( {\begin{array}{*{20}{c}}a&0&0\\0&b&0\\0&0&c\end{array}} \right)\] Veamos qué característica especial presentan las potencias de una matriz diagonal: \[{D^2} = D.D = \left( {\begin{array}{*{20}{c}}a&0&0\\0&b&0\\0&0&c\end{array}} \right).\left( {\begin{array}{*{20}{c}}a&0&0\\0&b&0\\0&0&c\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{{a^2}}&0&0\\0&{{b^2}}&0\\0&0&{{c^2}}\end{array}} \right)\] \[{D^3} = D.D.D = \left( {\begin{array}{*{20}{c}}{{a^2}}&0&0\\0&{{b^2}}&0\\0&0&{{c^2}}\end{array}} \right).\left( {\begin{array}{*{20}{c}}a&0&0\\0&b&0\\0&0&c\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{{a^3}}&0&0\\0&{{b^3}}&0\\0&0&{{c^3}}\end{array}} \right)\] En general: \[{D^k} = \left( {\begin{array}{*{20}{c}}{{a^k}}&0&0\\0&{{b^k}}&0\\0&0&{{c^k}}\end{array}} \right)\;\;,\;\;\;\;\;\;k \in \mathbb{N}\]
Matrices escalares
Una matriz escalar es una matriz diagonal en la cual todos los elementos de la diagonal principal son iguales.
Las matrices escalares de orden 3 tienen esta forma:
\[E = \left( {\begin{array}{*{20}{c}}k&0&0\\0&k&0\\0&0&k\end{array}} \right)\;\;,\;\;\;k \in \mathbb{R}\]
\[E \in {\mathbb{R}^{n \times n}}\;es\;escalar \Leftrightarrow E = kI\;\;,\;\;\;k \in \mathbb{R}\]
Matrices ortogonales
Una matriz cuadrada es ortogonal cuando su traspuesta coincide con su inversa:
\(A \in {\mathbb{R}^{n \times n}}\) es ortogonal \( \Leftrightarrow {A^t} = {A^{ – 1}} \Leftrightarrow A{A^t} = I \wedge {A^t}A = I\)
Por ejemplo las siguientes matrices son ortogonales:
\[A = \left( {\begin{array}{*{20}{c}}{\frac{1}{{\sqrt 2 }}}&{ – \frac{1}{{\sqrt 2 }}}\\{\frac{1}{{\sqrt 2 }}}&{\frac{1}{{\sqrt 2 }}}\end{array}} \right)\;\;\;\;\;\;,\;\;\;\;B = \left( {\begin{array}{*{20}{c}}{\frac{1}{{\sqrt {10} }}}&{\frac{3}{{\sqrt {10} }}}\\{\frac{3}{{\sqrt {10} }}}&{ – \frac{1}{{\sqrt {10} }}}\end{array}} \right)\]
Dejamos a cargo del lector verificar que las matrices cumplen la definición.
Observemos que las columnas de \(A\) y de \(B\) son vectores ortogonales y de módulo \(1\). Ésta es la característica que distingue a las matrices ortogonales.

